グラフ理論は、点(ノード)と線(エッジ)で、関係性を表す抽象化された概念です。
本記事では、グラフ理論の概要を紹介します。
グラフ理論の概要を紹介します
- グラフ理論とは
- グラフ理論の構成要素
- グラフの種類
- グラフ理論の使い方
グラフ理論の概要
グラフ理論は、点(ノード)と線(エッジ)で、関係性を表す抽象化された概念です。
グラフ理論によって、人間関係やネットワーク、処理フロー、路線図などを表現することができます。
図


グラフ理論の構成要素
グラフ理論では、点(ノード)と線(エッジ)で関係性を表現します。
| 要素 | 図 | 内容 |
|---|---|---|
| 点(ノード) | ○ | 対象のものを示す |
| 線(エッジ) | ─ → | 関係性を示す |
グラフの種類
グラフの種類を紹介します。
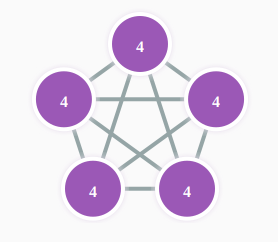
完全グラフ
完全グラフは全てのノード同士にエッジがあるグラフです。
図


正則グラフ
正則グラフはノード同士のエッジ数が等しいグラフです。
図

無向/有向グラフ
無向グラフと有向グラフを紹介します。
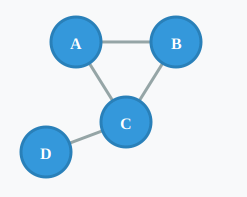
無向グラフ
無向グラフは双方向関係のグラフです。
人間関係やネットワーク等を示すことができます。
図

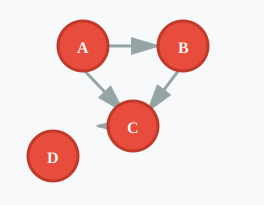
有向グラフ
有向グラフは向き有りのグラフです。
処理フローや依存関係を示すことができます。
図

循環/非循環グラフ
循環グラフと非循環グラフを紹介します。
循環グラフ
循環グラフは閉路のあるグラフです。
図
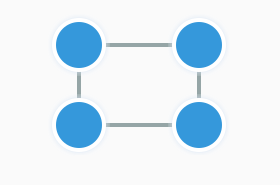

非循環グラフ
非循環グラフは閉路のないグラフです。
図
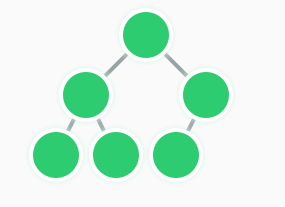

オイラーグラフ
オイラーグラフは、一筆書きして、戻れるグラフです。
全てのエッジを通り、始まりのノードに戻ってくることができるグラフです。
図
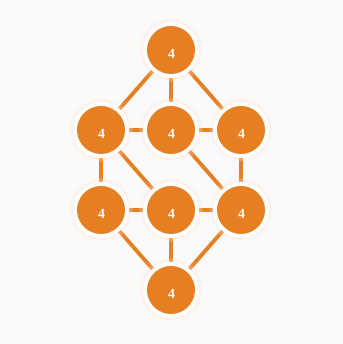

ハミルトングラフ
ハミルトングラフは、全てのノードを通り、戻れるグラフです。
図


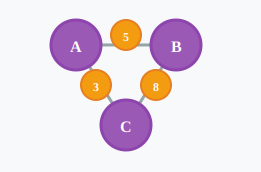
重み付きグラフ
重み付きグラフは重み(コスト)のパラメータを付与したグラフです。
距離を重みとした路線図等を表現することができます。
図

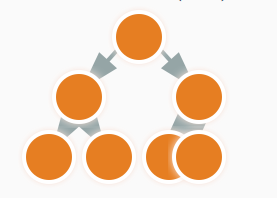
DAG(Directed Acyclic Graph)
DAGは循環しない有向グラフです。
一方向にしか進めない特徴があるグラフです。
データ処理フローを示すことができるため、エンジニアリングでもたびたび利用されます。
図

グラフ理論の使い方
グラフ理論は、設計を整理するために利用することができます。
また、状態遷移の管理に、グラフ理論を利用することができます。
エンジニアリングによるグラフ理論の使い方を紹介します。
設計の整理
条件分岐(if文)が多く、処理が煩雑になってしまった場合、グラフで表現すると、処理内容を整理することができます。
依存関係の整理
ソフトウェアの依存関係や、処理手順の依存関係をDAGとして表すことができます。
探索
処理変更の影響範囲の特定や、デバッグ影響を表すことができます。
最適化
コスト計算や、処理時間の計算を、重み付けグラフを用いて算出することができます。
状態遷移の管理
ワークフローを、グラフ理論で実装することができます。
LangGraph、Dify、GraphAIでは、グラフ理論を用いて実装することができます。
まとめ
グラフ理論の概要を紹介しました。
- 点(ノード)と線(エッジ)で関係性を表す
- グラフには種類がある
- エンジニアリングで利用することができる
グラフ理論は、点(ノード)と線(エッジ)で関係性を表すことができます。
条件分岐(if文)が多く、処理が煩雑になってしまった場合、グラフで表現すると、処理内容が整理されるので、グラフ化することを推奨します。
条件分岐処理自体をグラフで定義して、処理することも可能なため、グラフ理論はエンジニアとして覚えておきたい理論の1つです。

